Белов Н.Н. Доклад на соискание научной степени доктора физико-математических наук - без защиты диссертации - ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ДАВЛЕНИЯ В ЦИКЛОНАХ, СМЕРЧАХ И ШАРОВЫХ МОЛНИЯХ АЭРОДИНАМИЧЕСКОЙ ПРИРОДЫ

Белов Николай Николаевич,
Карачевская ООШ Козловского района
Чувашской Республики

ГИДРО - И АЭРОДИНАМИЧЕСКОЕ ДАВЛЕНИЕ
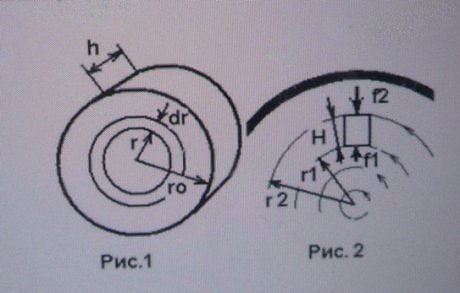
Вначале нашего доклада приведем общеизвестный расчет жидкости или газа плотности ρ на боковую поверхность герметически закрытого цилиндрического сосуда высотой h с радиусом оснований r , вращающегося стационарно и равномерно с угловой скоростью ω вне поля тяготения как твердое тело вокруг оси симмерии (см. Рис.1)



Для расчета давления разобъем цилиндр на совокупность полых цилиндров одинаковой высоты h толщиной стенок dr, во много раз меньший r, тогда можно считать, что все точки выделенного полого цилиндра находятся на расстоянии r от оси. В выделенном объеме dv = 2πrdrh заключена жидкость или газ массой dm = ρ2πhrdr. Этой массе жидкости сообщает центростремительное ускорение сила давления слоя, находящегося на расстоянии r + dr от оси. Согласно второму закону Ньютона df = dmdυ/dt , т.к. dυ/dt = ω r.
Динамическое давление, производимое выделенным слоем жидкости или газа на внешнюю боковую поверхность полого цилиндра dp = df/ds, где ds= 2πrh. – площадь боковой поверхности этого полого цилиндра.
С учетом всех указанных выше равенств находим элементарное давление:
dp=ρω rdr (1)
Суммарное давление, производимое всеми слоями вращающейся жидкости найдем, взяв определенный интеграл:
p = ρω rdr = 0,5ρ ω r . (2) Или, заменив в полученном выражении поизведение угловой скорости на радиус окружности через линейную скорость υ = ωr имеем:
р = 0,5ρυ . (3 )

ЗАВИСИМОСТЬ ГИДРОДИНАМИЧЕСКОГО ДАВЛЕНИЯ ОТ ТОЛЩИНЫ ВРАЩАЮЩЕГОСЯ
СЛОЯ ЖИДКОСТИ ИЛИ ГАЗА
Выражения (2) и (3) выведены для случая, когда жидкость или газ целиком заполняют сосуд. Рассчитаем давление жидкости или газа толщиной потока . Рассмотрим два разных случая а) частицы вращаются с одинаковой угловой скоростью, тогда в выражении (2) следует изменить нижнюю границу интегрирования:
р = ρω r dr = ρω 0,5(r + r ) (r - r ). (4)
Итак, в этом случае гидродинамическое давление прямо пропорционально плотности, квадрату угловой скорости, толщине потока (r - r ) и радиусу кривизны среднего слоя – 0,5(r + r ).
Если частицы потока имеют одинаковую скорость, например, совершая отражение, давят на лопасти турбины Пельтона при трогании с места, тогда в выражении 1 угловую скорость выразим через линейную скорость и радиус кривизны ω = υ/r. При взятии интеграла (2) вынесем за знак интеграла плотность и линейную скорость. Давление в этом случае будет:
p = ρυ = ρυ ln . (5)
Из этого выражения видно, что гидродинамическое давление прямо пропорционально плотности, квадрату линейной скорости и натуральному логарифму отношения радиусов кривизны поверхностей слоев, между которыми заключен поток. Заметим, что математический запрет r не равен нулю имеет реальный физический смысл – изменение импульсов частиц потока не происходят моментально и точно по ломаным линиям, а по сопряженным.
Сила давления на неподвижную лопасть турбины:

F = s ρυ ln . (8)
, где s – площадь проекции рабочей части лопасти на пепендикулярную к начальной скорости частиц потока.
Если лопасть турбины наберет скорость υ относительно земли, то поток приближается к лопасти со скоростью υ - υ , то именно этой относительной скорости зависит прямо пропорциональна сила давления
F = s ρ(υ- υ ) ln . (9)
Мощность турбины равна изменению кинетической энергии потока за единицу времени:
N = F υ = s ρ υ (υ- υ ) ln . (10)



ВЫВОД ОСНОВНОГО УРАВНЕНИЯ МОЛЕКУЛЯРНО-КИНЕТИЧЕСКОЙ ТЕОРИИ ИДЕАЛЬНОГО – РАЗРЕЖЕННОГО ГАЗА
Выражение /3/ справедливо для жидкости и газа, слои которых непроницаемы для слоев, более удаленных от оси вращения, а в случае разреженного газа слои, близлежащие к стенке сосуда радиуса r проницаемы, поэтому при взаимодействии со стенкой молекулы, имеющие проекцию скорости на радиальную ось описывают дуги одинакового радиуса r , следовательно произведение плотности на квадрат угловой скорости и на радиус r можно вынести за знак интеграла в выражении /2/ , тогда
среднее давление p = ρυ , т.к. υ = 1/3 υ , тогда получим: p = 1/3 ρυ .

ЦЕНТРОСТРЕМИТЕЛЬНО- ВЫТАЛКИВАЮЩАЯ – ГИДРО-АЭРОДИНАМИЧЕСКАЯ АРХИМЕДОВА СИЛА.
На более удаленную и перпендикулярную к радиусу r грань небольшого тела, находящегося во вращающемся потоке (см. Рис. 2) действует
большее динамическое давление
f =0,5ρω r s- эта сила давления больше, чем на противоположную грань
f = 0,5 ρω r s , а на другие попарно-противоположные грани действуют одинаковые силы давления, попарно компенсирующие друг-друга, поэтому результирующая всех сил давлений направлена к оси вращения и является гидродинамической Архимедовой силой:
F = ρω (r + 0,5H)Hs. (11)
выражение, стоящее в скобках –это радиус, проведенный к центру масс тела, а высота тела равна разности радиусов Н= r - r ;
m =ρHs – масса вытесненной жидкости;
ω (r + 0,5Н) – центростремительное ускорение частиц, окружающих тело.
Итак, Гидродинамическая Архимедова сила равна по модулю произведению массы вытесненной телом жидкости или газа на центростремительное ускорение окружающих его частиц среды.
Ярким проявлением такой Архимедовой силы объясняется движение чаинок к области оси вращения – чем больше квадрат угловой скорости вращения, тем быстрее чаинки достигают центра дна чашки.
Принцип действия центрифуги и сепаратора объясняется тем, что если пренебречь действием силы тяжести на тело, то согласно второму закону Ньютона
F = ma = ρ sH , где ρ - плотность тела и оно
оно получает ускорение а под действием центростремительно направленной гидродинамической Архимедовой силы:
F = ρ ω (r + 0,5H)Hs.
Приравняв левые части равенств и сократив на объем тела sH получим:
a = ρ ω (r + 0,5H)/ ρ . (12)
Из этого выражения видно, что если плотность примеси меньше плотности жидкости, то ускорение тела больше ускорения частиц жидкости, равной ω (r + 0,5H) и вытесняется к центру, что и поясняет принцип сепарации.
Если плотность примеси больше плотности жидкости, то его ускорение меньше ускорения частиц среды, следовательно он удаляется от оси вращения, накапливается на стенке центрифуги.
Если упомянутые плотности равны, то такая примесь не отделима сепаратором или центрифугой.


ФУНКЦИЯ РАСПРЕДЕЛЕНИЯ ПЛОТНОСТИ И ДАВЛЕНИЯ ВОЗДУХА В ЦИКЛОНАХ, СМЕРЧАХ И ШАРОВЫХ МОЛНИЯХ
При больших угловых скоростях стационарного вращения газа - воздуха в выражении (1) нельзя его плотность ρ считать везде одинаковой, следует учесть его сжимаемость.
На произвольном расстоянии r плотность ρ воздуха можно выразить через равление р, молярную массу М = 0,029 кг/моль, газовую постоянную R=8,31 Д/моль К и абсолютную температуру Т из уравнения Менделеева-Клапейрона: ρ = pМ/RT. Т примем примерно равным 300К.
Найдем дифференциал плотности dρ воздуха через дифференциал давления dp, считая, что при стационарном вращении температура Т примерно везде одинакова:

dρ = dp M/RT. (13)

С учетом уравнения /1/ получим дифференциальное уравнение с разделяющимися переменными:

dρ/ρ = Mω rdr/RT. (14)

Учитывая, что r = 0 для центральной области плотность ρ = р М/RT , где р – искомое давление в центральной области, а на расстоянии r – на границе циклона или смерча давление р примерно равно нормальному атмосферному давлению 100000 Па, возьмем определенные интегралы от обоих частей:

dρ/ρ = Mω /RT rdr и получим:
ln ρ/ρо = Mω r / 2RT = Мυ /2RT, или окончательно:

ρ = ρо ехр ( Мυ /2RT) . (15)

Выразив дважды плотность газа через давление и сократив на М/RT имеем:

р = ро ехр (Мυ /2RT). (16)

Из последнего выражения видно, что степень разрежения воздуха в центральной области циклона и смерча тем больше, чем больше отношение Мυ /2 – кинетической энергии механического обращения одного моля газа вокруг оси вихря ( циклона или смерча ) к энергии RT – энергии теплового движения одного моля, приходящаяся на две степени свободы.
Т.к. молярная масса газа равна произведению массы одной молекулы m число Авогадро N , а универсальная газовая постоянная R равна произведению постоянной Больцмана k на число Авогадро N , то после сокращения на N выражение (16) записывается через среднюю кинетическую энергию направленного вращения одной молекулы вокруг оси вихря mυ /2 к величине kT- энергии теплового движения молекул, приходящаяся на две степени свободы:
р = ро ехр (Емех/kT). (17)
Как известно, если угловая скорость всех частиц вихря одинакова, то линейная скорость их обращения пропорциональна по модулю радиусу-вектору, поэтому в таблицах распределения давления внутри циклонов и смерчей мы дали для областей, положение которых можно задать в долях радиуса.
По нашим расчетам получены следующие таблицы (см. ниже) , в первых строках которых указаны расстояния в r/rо – в долях радиуса от оси вихрей; во вторых строках – линейная скорость ветра в м/с; в третьих – давление в гектопаскалях.
На рис. 3 представлены графики распределения давления 1 - в циклоне-урагане с максимальной скоростью ветра 50 м/с на границе со спокойным воздухом; 2 – в смерче с максимальной скоростью 200 м/с на границе; 3 – при 500 м/с; 4 – при 1000 м/с – мы полагаем, что примерно с такой скоростью движутся частицы воздуха на границе шаровой молнии – т. е. их скорость механического обращения сравнима и даже больше максимальной скорости теплового движения молекул.

Обратим внимание на то, что в граничной области этих феноменов природы большой перепад давления на единицу вдоль радиуса – т.е. большой градиент давления – особенно в смерчах и шаровых молниях. Вот почему в смерчах на тела действует очень большая Аэродинамическая Архимедова сила. Приведем пример расчета давления в центральной области циклона, в периферии которой скорость ветра 50м/с.
Согласно расчетной формуле 8 с учетом того, что давление на границе вихря равно примерно нормальному атмосферному давлению р=100000 Па, молярная масса воздуха М=0,029 кг/моль, а абсолютная температура Т=300К.
р =100000ехр(- 0,029х2500 / 2х8,31х300) = 985556 Па.
Теперь, зная это давление, можно рассчитать давление внутри циклона на любом расстоянии от оси вращения и получим таблицу:
Табл. 1 Распределение давления в циклонах и штормах
Расстояние от центра в долях радиуса r/rо 0 0,2 0,4 0,6 0,8 1
Линейная скорость
ветра υ, м/с 0 10 20 30 40 50
Давление р,
гПа
985 986 987 990 994 1000


Табл.2 Распределение давления в ураганах
r/rо 0 0,2 0,4 0,6 0,8 1
υ,м/с 0 40 80 120 160 200
р, гПа 820 830 845 890 940 1000

Табл.2 Распределение давления в смерчах
r/rо 0 0,2 0,4 0,6 0,8 0,9 1
υ,м/с 0 100 200 300 400 450 500
p,гПа 234 248 294 394 592 759 1000

Табл. 3 Распределение давления в шаровых молниях
r/rо 0 0,2 0,4 0,6 0,8 0,9 1
υ,м/с 0 200 400 600 800 900 1000
р, гПа 3 35 70 150 320 530 1000

Табл. 4 Давление в приосевой области вихрей, запертых снизу поверхностью Земли
υ, м/с 0 50 100 200 400 600 800 1000
Ро, гПа 1000 985 943 792 394 123 24 3

Табл. 5 Распределение давления в ультрацентрифуге-компрессоре с открытой приосевой областью – давления 1 атм. и с вихревой камерой, заполненной пористым материалом для того, чтобы давление «не играло» из-за возможного выброса газа через приосевую область при наступлении детонации).

r/rо

υ, м/с р, атм.
0 0 1
0,02 20 1,002
0,04 40 1,009
0,06 60 1,021
0,08 80 1,038
0,1 100 1,06
0,2 200 1,26
0,4 400 2,54
0,6 600 8,12
0,8 800 41,36
1,0 1000 336
Вышеупомянутую, но герметически закрытую, вихревую камеру можно использовать в качестве вакуумного насоса если, на стенках выполнить микроскопические отверстия с клапанами.
На основе анализа таблицы 4 полезно рассчитать - при какой скорости частиц граничной области шаровой молнии давление в центральной области близко к нулю, например, равен 1 Па.
Для этого обе части уравнения 8 разделим на ро и возьмем от обеих частей равенства натуральный логарифм и получим:

ln(р/ро) = Мυ / 2RT , откуда имеем:

υ = (2RTln(p/ро)/M) . (18)
после подстановки численных значений получим: υ=1407м/с. Следовательно, расчет показал, что в нашей модели - «шаровая молния – вакуумная бомба – шарообразный замкнутый вихрь воздуха, на «поверхности» которого молекулы движутся со скоростью, значительно большей скорости теплового движения».



ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ
СКРОСТИ ДВИЖЕНИЯ ЧАСТИЦ В СМЕРЧАХ
В том же журнале на – с.20 сказано: «Зарегистрирован случай, когда во время прохождения смерча сосновая палка пробила лист железа толщиной около сантиметра».
Обозначим эту толщину через h =0,01м. Площадь поперечного сечения палки обозначим через s, а массу ее выразим через объем и плотность: m = ρsl, где l – ее длина. Плотность сосны /2 - С.57/ примем примерно
ρ= 500кг/м . О длине палки ничего не сказано, ее примем длине годового среднего прироста l = 0,2м
В данном случае ее кинетическая энергия 0,5ρslυ примерно равна затратам энергии - на работу по пробиванию отверстия той же площади поперечного сечения, которую можно выразить через предел прочности (σ=2 10 Па) железа σsh, тогда получим равенство:
0,5ρslυ = σsh, сократив обе части равенства на s получим формулу для расчета скорости ее совместно с окружающими ее частицами среды:
υ = (2σh/ρl) , после подстановки численных значений величин получим: υ = 200 м/с.
Вывод: расчет подтвердил наше предположение о скорости движения частиц в граничной области смерчей.

ЭКСПЕРИМЕНТАЛЬНОЕ ОПРЕДЕЛЕНИЕ
МАКСИМАЛЬНОЙ СКОРОСТИ ЧАСТИЦ В СМЕРЧАХ

На рисунке-фотографии 10 того же журнала изображена рейка, проткнувшая ствол пальмы – почти точно сквозь сердцевину. В справочниках нет данных о плотности и прочности древесины этого дерева, но известно, что его плотность не более 1000кг/м . Как известно, рейки после распила древесины теряют влагу, примем плотность рейки ρ=640кг/м , т.е примерно как у березы влажностью 15%. Определим примерно диаметр ствола пальмы на высоте, где она проткнута. Центр входного отверстия рейки на рисунке находится примерно на таком же угловом расстоянии – 45 от поверхности станицы, что и от перпендикулярной плоскости к этой станице, мысленно проведенная через сердцевину пальмы, поэтому размер толщины рейки на плоскость рисунка составляет 0,5 = 0,71 часть реального. Если предположить, что толщина рейки 2см, то ее проекция на плоскость рисунка равна =1,41см. На фото эта толщина изображена размера 0,8мм, а ствол на фото имм\еет размер 7,7мм, т.е 9,6 раза больший, умножив его на 2 получим истинный диаметр пальмы, равный глубине отверстия D= 19,2см=0,192м.
Массу рейки выразим через плотность и объем:
M = ρsl, где s=10cм ; l = 86cм (найдено также из рисунка).
И в этом случае большая часть кинетической энергии, разогнанной в смерче идет на «выбивание» отверстия, но на этот раз на основе предварительного эксперимента рассчитаем работу на сверление этого отверстия объемом
V = sD=10х19,2 см = 192см
В березовом бруске толщиной h=4,6см помощью коловорота с радиусом колена
r = 0,1м, прилагая к ручке перпендикулярно к плоскости колена силу F=30 Н мы при сверлении отверстия диаметра 1,2см совершили n=32 оборота и совершили работу А = 2π r n F = 603 Дж. Объем нашего отверстия v = πd h/4 = 5,2 см . Энергия, затраченная рейкой на выбивание отверстия, по крайней мере в 192: 5,2 = 37 раз больше нашей работы по сверлению небольшого отверстия т.е. составляет Е=37А=22311Дж.
Поэтому имеем равенство: 0,5ρslυ = Е, откуда находим скорость

υ= ( 2Е/ρsl) , подставив численные значения величин получим: υ= 285 м/с. – это еще более жесткий смерч!
Если учесть, что рейка не только проткнула ствол пальмы, но и «вдавила» до ее половины и учесть, что рейка - не сверлила, а пробила отверстие, при этом если даже предположить, что при проникновении на каждые 5 см сила сопротивления увеличивалась вдвое, то к моменту выхода она увеличилась бы два в четвертой степени раз! Если учесть, что на рисунке-фото изображено живое дерево, содержание влаги в ней велико и плотность может быть больше 800кг/м и очень трудно представить сам «процесс механического вхождения рейки в сырое дерево – пальму» - ведь сжимаемость сырой древесины мала, ствол сырого дерева должна просто рассыпаться как бутыль, заполненная водой.
По нашему мнению единственно вазможный вариант – внедрение конца рейки происходило по мере быстрого испарения влаги вместе с частицами древесины по мере движения.
Рассчитаем, при какой скорости вышеупомянутой рейки выпарилась вода и другое содержимое на месте будущего отверстия.
Согласно закону сохранения энергии кинетическая энергия рейки примерно вся пошла на нагревание и парообразование воды, которое можно записать в виде следующего равенства:
0,5 m υ = cmΔT + L m ,
где удельная теплоемкость воды с= 4200Дж/кг; ΔT=73К; Удельная теплота парообразования воды L=2257000 Дж/кг. Для простоты расчета допустим, что рейка из сырой пальмы. Из рисунка нетрудно определить, что длина рейки в 4,3 раза больше диаметра ствола дерева, тогда масса стоящая в левой части больше 4,3 раза больше массы воды, которая нагрелась и испарилась, тогда обе части равенства сократим на массу m и выразим скорость начального движения рейки и окружающих его частиц:
υ =[(cΔT + L)/4,3] .
После подстановки значений величин получаем:
υ = 772 м/с. Итак, в смерчах скорость обращения частиц в области, близкой к граничной, достигает сотен метров в секунду – сравнима со скоростью теплового движения молекул воздуха, например, средняя скорость теплового движения молекул азота при температуре
300 К равна  :
υ=(3RТ/M) = 517 м/с.

ОБ ЭЛЕМЕНТАХ СТРУКТУРЫ СМЕРЧЕЙ
На рисунке 5, упомянутой Л.Алексеевой «О вихрях…» (см. ж. Квант, №3.- 1977. – С.18) представлена фотография внутренней полости смерча, снятая снизу. На этой фотографии четко видно, что стенка смерча имеет биспиральную структуру – можно предположить, чо в этой области частицы совершают вращение вокруг «тонкой» спирали, «сложенную» в другую спираль, образующую стенку смерча. Такая же биспиральная структура внешней стенки, видимая в отраженном свете изображена на Рис.6 – фото и даже в зарисовке центрального смерча - рисунок 8. Очень интересна и весьма полезна для нас следующие сведения из статьи Алексеевой: «Однажды нижний край смерча прошел над головой наблюдателя на высоте 6 м. Ширина внутренней полости этого смерча была около 130 м, тогда как толщина стенки – всего 3 м …позже смерч прошел над наблюдателем и опустился к земле, коснулся соседнего дома и в одно мгновение унес его. Дом распался в воздухе».
Оценим «толщину стенки» смерча. Из графика 4 распределения давления в смерче видно, что граничный слой толщиной 0,1 от r/rо производит давление, больше половины давления, производимого остальными – внутренними слоями. Мы считаем, что именно этот слой обладает наибольшей кинетической энергией и разрушительной силой. При диаметре около 130 метров толщина этого слоя составляет примерно 13 метров. У нас возникает сомнение – смог ли упомянутый выше наблюдатель с такой точностью определить «толщину стенки». Мы считаем, что невооруженный глаз заметил только тот слой стенки – темный слой, в которую извне проникает воздух, содержащий водяной пар, который адиабатно расширяется, охлаждается и переходит в критическое состояние с образованием тумана – именно он визуален. Следовательно, мы считаем, что из 13 метров 3 метра – это слой водяного тумана – темный на просвет, но хорошо отражающий свет – именно благодаяря этому видна на рисунке 5 биспиральная структура, а на рисунках 4 и 8 – видна внешняя поверхность видимой стенки смерча – она напоминает поверхность веревки, не противоречащая биспиральной структуре – нашему предположению. «Толщина стенки» смерча, изображенного на рисунке 5 примерно равна половине его радиуса. Рассмотрим, как может возникнуть биспиральная структура вихрей - не только смерчей, но и циклонов и штормов. В народе давно замечено, что при больших скоростях ветра, достигающих десятков метров в секунду возникает вьюга – факт неоднородности структуры потока ветра. На рисунке 1 – с.16 упомянутого нами журнала «Квант» (№8.-1977) , в котором стрелками показаны направления ветров в циклоне следует дать уточнение – стрелки – лишь оси вихревого движения воздуха в ветрах, ибо на рисунках 2 и 3 видны «отдельные прожилки более мелких спиралей» даже в области вернего – облачного слоя огромных спиралей.
Согласно закону сохранения момента инерции по мере «сжатия» диаметра циклона атмосферным Давление в центральных областях циклонов уменьшается не только из-за вращения, но и из-за конденсации и выпадения осадков.
Согласно закону сохранения момента инерции по мере «сжатия» диаметра циклона атмосферным давлением увеличивается частота вращения – в том числе и в мелких спиралях, охватывающих линии тока, и в периферии (см. нисходящие стрелки ветров рис.1) Попав в подоблачный слой интенсивность солнечного излучения резко уменьшается, температура начинает уменьшаться, начинается интенсивная конденсация и резкое уменьшение давления как внутри мелких спиралей, но и в центральной области «целого пучка» этих спиралей, а по мере сжатия всего пучка увеличивается частота вращения до наступления стационарного состояния. По нашему мнению «начальная стадия опускания конца хобота – лишь проявление начала конденсации в нисходящем потоке.
Обратим внимание (см.рис 9).на то, что конец спускающегося хобота смерча изогнут, более прозрачен заперт, и имеет острый кончик.
Алексеева утверждает: « В черной туче скрыта горизонтальная часть смерча – вихревое образование, вращающееся вокруг оси, вытянутой параллельно поверхности Земли….на высоте около 300м…она напоминала огромную извивающуюся змею».
Упоминается подобная «Змея», переходящая в смерч наблюдалась с Земли, наполненная водой, которую смерч высасывал из озера, но далее не описано, что же происходит с этой водой и смерчем.
Автор приходит к выводу: «Смерчи возникают в районах, где соприкасаются воздушные массы с резко отличными тепловыми свойствами, в области мощных вертикальных движений и сходящихся потоков».
В подтверждение этого вывода можно добавить, что видимо такие потоки возникают в области высокой возвышенности между двумя сходящимися долинами или глубокими оврагами, причем один из них нисходит в направлении с юга на север, а другой с запада на восток – случайно ли это? Согласно народной молве Козловского района одна деревня исчезла из-за того, что именно на горе стыка двух долин дома подвергались разрушениям ураганами и смерчами – через несколько десятков лет территория этого участка была выделена под дачи – теперь страдают дома дачников – не часто, но нападки смерчей бывают.
В деревне Картлуево Козловского района Чувашии смерч с горы между глубоким оврагом и долиной реки Аниш снес крышу сарая новосельца – новой молодежной улицы и поставил в западную долину. Интересно заметить, что вокруг мощного смерча могут двигаться в том же направлении менее мощные – в тот же день Петрикова Е вышла в огород и увидела как вихрь воздуха поднял плети вместе с огурцами с грядок и рывками дергал их вверх – не выдернул, но дергал! Она сильно испугалась и быстрее зашла в дом. Этот факт говорит о том, что в центральной области вихрей возникает быстро восходящий поток воздуха.
Мы думаем, что когда нижний конец смерча закрыт поверхностью Земли такого потока нет, а когда этот конец внутри с давлением, значительно меньшим атмосферного «встретит» неровности, например, растительность или даже строения, в которых давление равно атмосферному поток воздуха устремляется в центральную область и поднимет и уносит тела и строения. Двигаясь вверх и попав в область пониженного давления, воздух расширяется, разрушая и разбрасывая их на отдельные части.

ГИПОТЕЗЫ О ПРИРОДЕ СМЕРЧЕЙ
Возникает вопрос – за счет какой энергии увеличивается и поддерживается долгое время мощь смерча?
Во-первых мы считаем, что в тех случаях, когда смерч резко сжимается работа сил атмосферного давления идет на увеличение механической энергии не всего смерча, а прежде всего слоев, ближайших к граничным из-за того, что адиабатное расширение внешних слоев во внутренние вдоль радиального направления и против потока частиц невозможна, поэтому это расширение происходит вдоль направления обращения частиц потока больших скоростей после «толчка давления», т.е происходит прямое превращение работы сил давления в механическую энергию вращения потоков смерча.
Во-вторых, при больших скоростях обращения частиц граничных слоев смерча непрерывно происходит прямое преобразование части внутренней энергии окружающего воздуха в механическую энергию и диссимиляция молекул окружающего воздуха по направлениям и по скоростям – молекулы, имеющие тепловую скорость, не меньшую скорости движения частиц смерча, направленные по касательной или внутрь под небольшим углом к внешним слоям смерча проникают в эти слои, увеличивая тем самым кинетическую энергию потоков смерча, а те молекулы воздуха, которые движутся вдоль касательной или под острым углом протвоположно направлению движения частиц смерча или приближаются к смерчу вдоль радиальной прямой отражаются обратно, но часть их импульса все равно передается слоям смерча, поэтому они « превносят свой вклад» в сохранении формы и размеров горизонтального сечения смерча.
Третья гипотеза –«стенка смерча» имеет биспиральную структуру».
Четвертая гипотеза - внутренние области смерча с частицами дотепловых скоростей «катятся» на биспиралях как на шариках.
Пятая гипотеза – при скоростях обращения частиц вокруг оси смерча, сравнимых с тепловой скоростью молекул биспирали распадаются сливаясь и образуя снаружи смерча тонкий и противоположно
обращающийся поток формы стенки цилиндра.

ОПЫТНОЕ ПОДТВЕРЖДЕНИЕ СОСТОЯТЕЛЬНОСТИ ЧЕТВЕРТОЙ ГИПОТЕЗЫ
На блюдце с водой поместим несколько пробок и в вытянутой руке равномерно совершим несколько оборотов вокруг вертикальной оси туловища – жидкость в сосуде вращается относительно удерживающей руки с периодом Т, равным периоду обращения сосуда совместно с пробками, сохраняющими взаимное положение, причем периодически превосходя скорость руки в положениях, ближайших к оси на 2πr/Т, где r- радиус окружности, описываемой пробкой.
В заключение отметим, что если суть второй гипотезы верна, то создание энергоустановки с турбиной в середине вихревых камер с искусственным смерчем нам представляется весьма актуальной.




ИНТЕРНЕТ-РЕСУРСЫ-ФОТОГРАФММ СМЕРЧЕЙ:

http://www.naturewallpaper.net/
wallpapers/
the_road_to_destruction___id_38844-2048x1536.jpg

http://bobrolet.ru/wp-content/gallery/winded/winded53.jpg